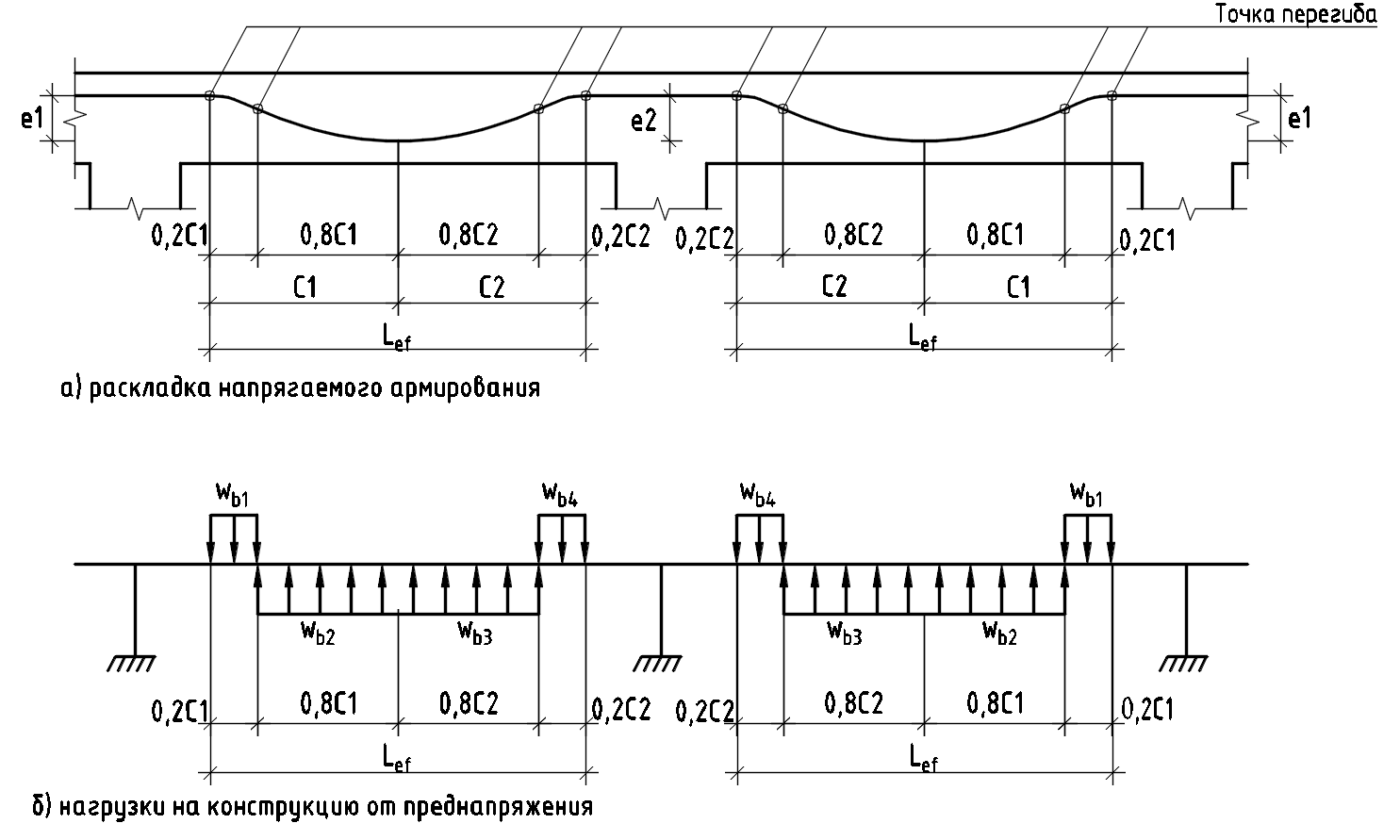
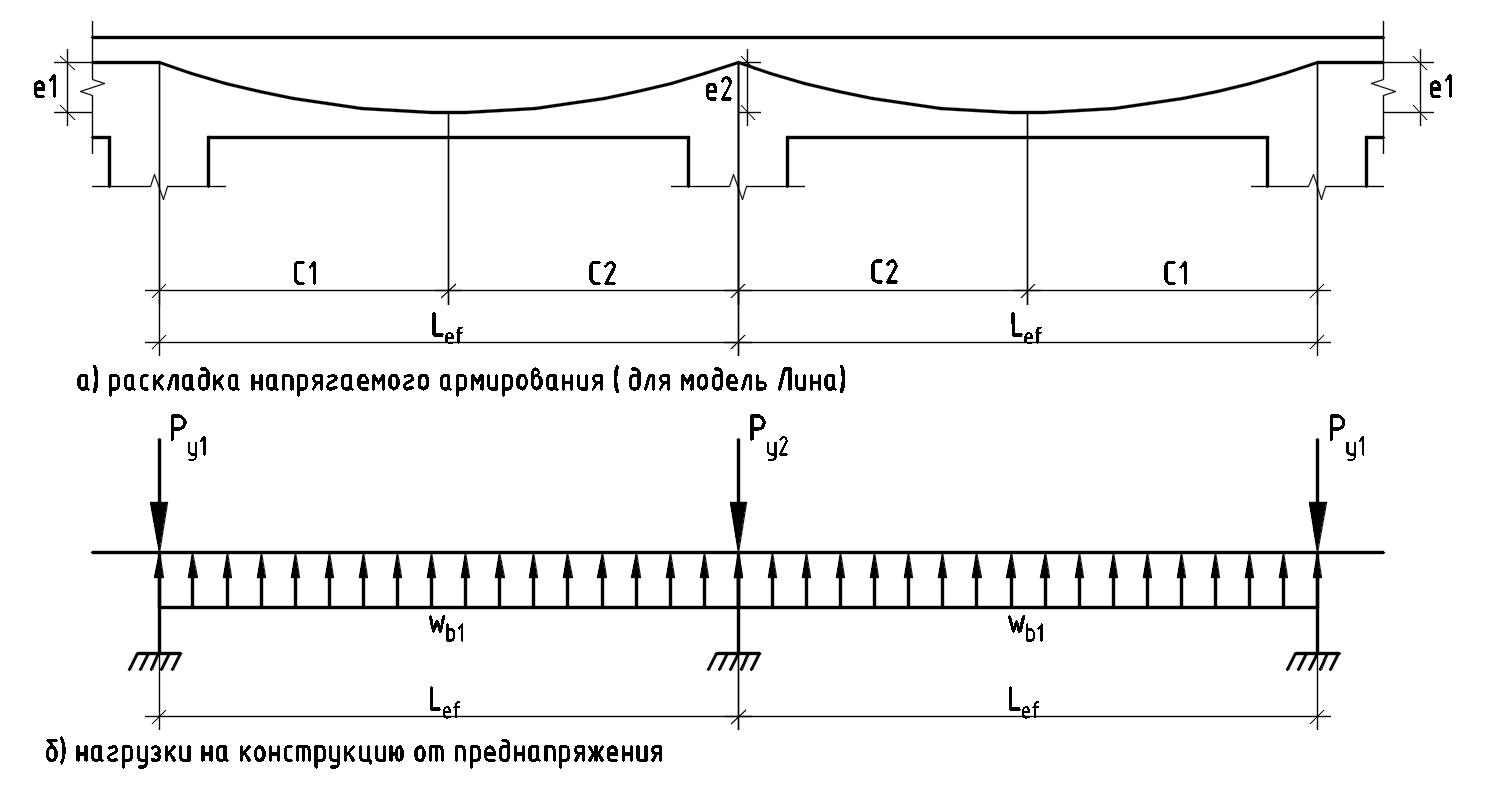
Моделирование нагрузки ПН
В настоящее время неотъемлемой частью проектирования является расчет конструкции в программных комплексах, реализующих метод конечных элементов.
В некоторых расчетных программах, например в ПК Sofistic, напрягаемая арматура задается специальными элементами, моделирующими систему предварительного напряжения. Действие преднапряжения на конструкцию, такие как обжатие и вертикальные воздействия, определяются для расчетной схемы автоматически.
Но в большинстве программных комплексов такой функционал отсутствует. В таком случае для определения усилий и деформаций в конструкции усилие от предварительного напряжения прикладывается как внешнее силовое воздействие. Существует три основных вида воздействия системы предварительного напряжения на конструкцию:
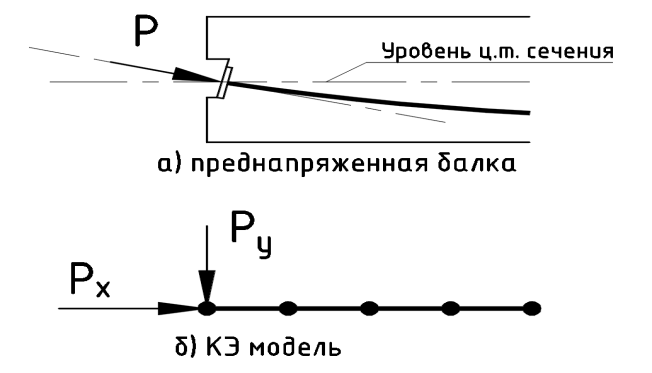
1. Сжимающая нагрузка на анкере – моделируется сосредоточенной силой в месте расположения анкеров. По направлению совпадает с касательной к оси пучка в точке расположения анкера.
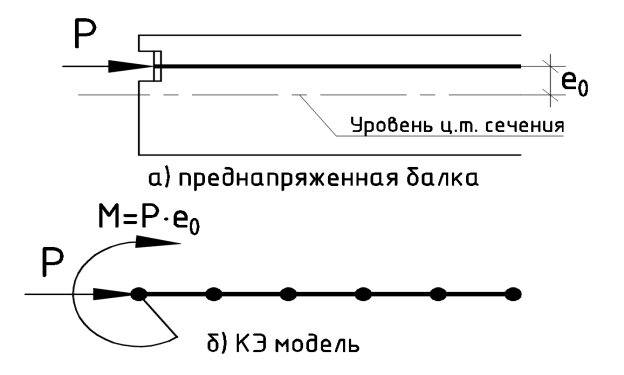
2. Момент от внецентренного расположения анкеров в сечении конструкции – моделируется сосредоточенной моментной нагрузкой в месте расположения анкеров. Значение момента определяется как произведение горизонтальной составляющей усилия обжатия на анкере на расстояние от центра анкера до центра тяжести сечения.
3. Вертикальные составляющие (отпор) при непрямолинейном расположении канатов по высоте – моделируются сосредоточенной или распределенной нагрузкой в местах перегиба высокопрочной арматуры.
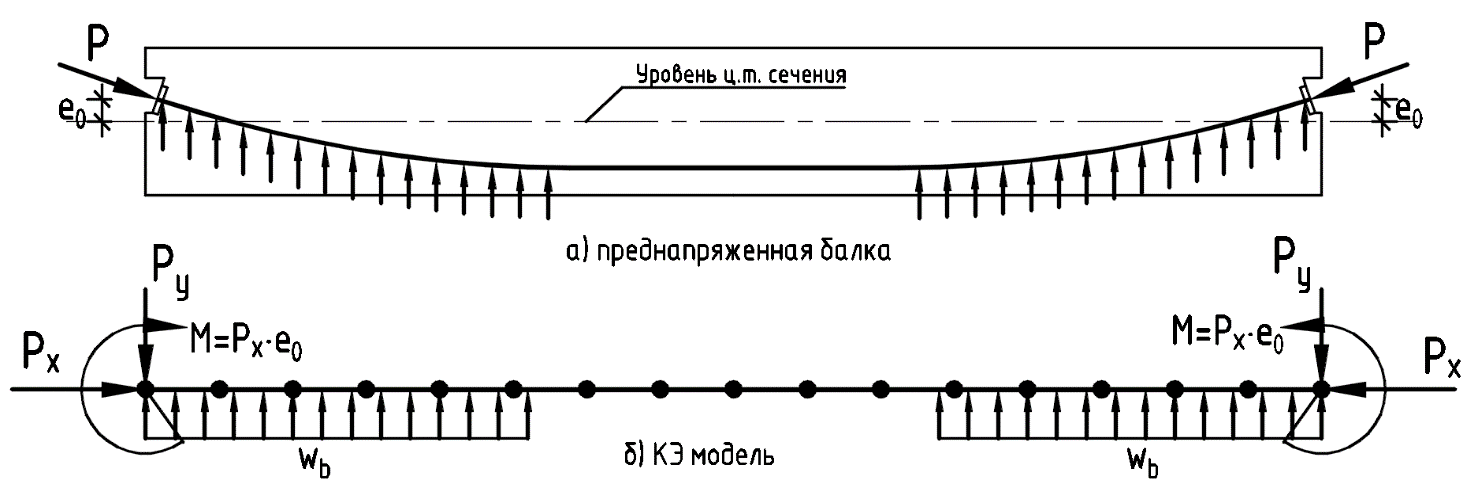
Вычисление вертикальной нагрузки от преднапряжения
При отгибе (изменении угла) напрягаемой арматуры в точке перегиба помимо осевых составляющих преднапряжения возникают также наклонные силы.
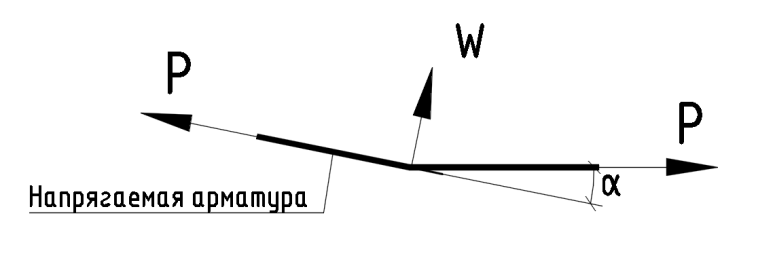
В общем случае при изменении угла наклона каната в точке на угол α вертикальная составляющая в этой точке будет равна Wу= P∙sinα.
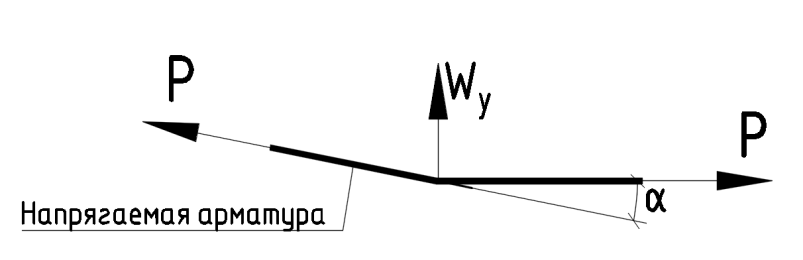
Вертикальная сила при перегибе напрягаемой арматуры.
Для удобства вычисления при малых углах наклона допускается силу Wy определять по формуле:
Wу= P∙tgα
где α - угол перегиба пучка.
Данная зависимость может быть использована для форм канатов, где длина участка пучка, на котором происходит перегиб, пренебрежительно мала. При этом необходимо обеспечение требования, при котором радиус изгиба каната в точке будет не менее допускаемого значения для данного типа каната или пучка.
Параболическая раскладка
Как правило, в конструкциях применяется раскладка напрягаемой арматуры по форме близкой к параболе. При подсчете вертикальной нагрузки от преднапряжения принимается, что по длине параболы действует равномерно распределенная нагрузка wb. Для одной ветви параболы нагрузка wb определяется по формуле:
wb = 2∙P∙e/l2
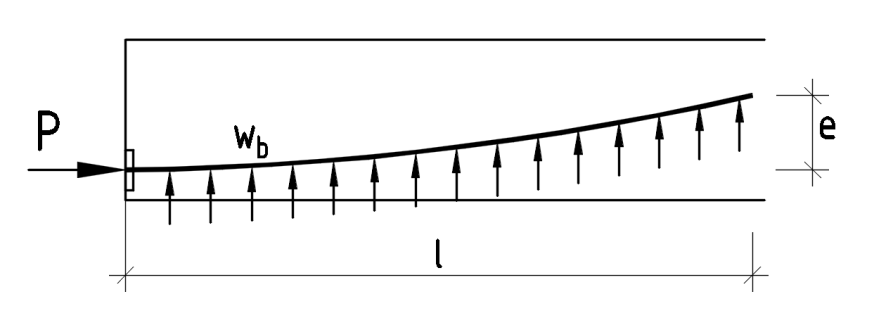
При параболической раскладке напрягаемой арматуры с двумя равными ветвями распределенная нагрузка wb определяется по формуле:
wb = 8∙P∙e/L2
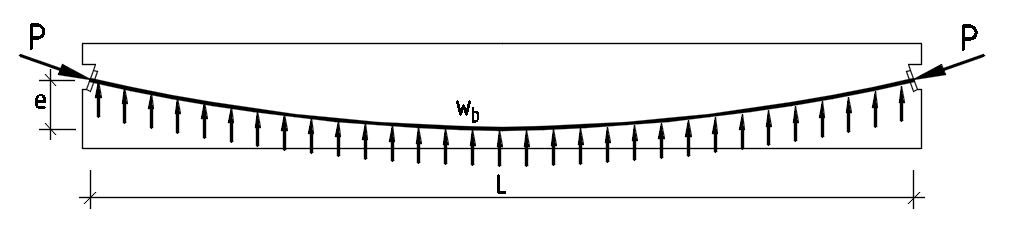
Зачастую парабола может состоять из двух частей разной длины и эксцентриситета. В таком случае каждая из частей параболы рассматривается отдельно.
В статически неопределимых конструкциях напрягаемая арматура раскладывается по форме, приближенной к эпюрам изгибающих моментов от равномерно распределенной нагрузки. Из условий конструирования соотношение высот (эксцентриситетов) криволинейных участков над опорой и в пролете обычно принимается как 2 к 8.
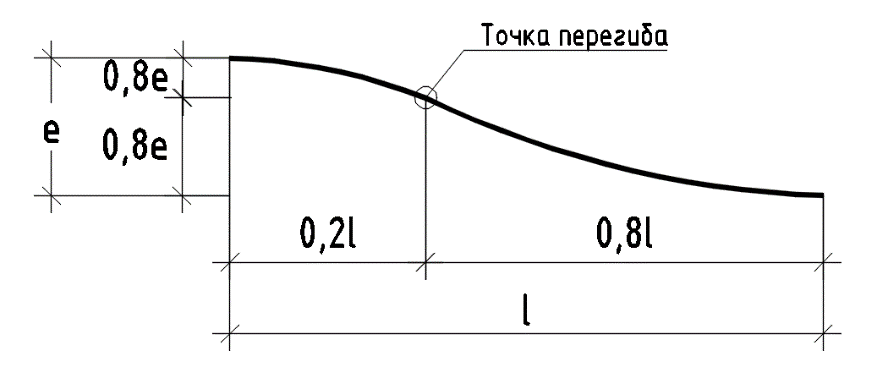
Данный тип раскладки напрягаемой арматуры для плит и балок позволяет добиваться оптимального распределения составляющих преднапряжения, а также позволяет в большинстве случаев избежать резких перегибов напрягаемой арматуры.
При расчетах фактическая раскладка в конструкции заменяется на идеализированную. Наиболее распространенная форма идеализированной раскладки подразумевает замену фактической геометрии каната в последовательность направленных вверх парабол и прямолинейных участков. Участок каната над колонной, где парабола направлена вниз заменяется точечной сосредоточенной силой. Впервые подобная модель была предложена в середине 1950-х годов американским ученым Т.И. Лином и получила название «модель Лина».